Цель работы состоит в том, чтобы узнать весь теоретический материал по теме «Вписанные и описанные многогранники» и научиться применять его на практике.

Многогранники, вписанные в шар Выпуклый многогранник называется вписанным, если все его вершины лежат на некоторой сфере. Эта сфера называется описанной для данного многогранника. Центр этой сферы является точкой, равноудаленной от вершин многогранника. Она является точкой пересечения плоскостей, каждая из которых проходит через середину ребра многогранника перпендикулярно ему.

Пирамида, вписанная в шар Теорема: Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.

Формула для нахождения радиуса описанной сферы Пусть SABC - пирамида с равными боковыми ребрами, h - ее высота, R радиус окружности, описанной около основания. Найдем радиус описанной сферы. Заметим подобие прямоугольных треугольников SKO 1 и SAO. Тогда SO 1/SA = KS/SO; R 1 = KS · SA/SO Но KS = SA/2. Тогда R 1 = SA 2/(2 SO); R 1 = (h 2 +R 2)/(2 h); R 1 = b 2/(2 h), где b - боковое ребро.

Призма, вписанная в шар Теорема: Около призмы можно описать шар только в том случае, если призма является прямой и около ее основания можно описать окружность.

Параллелепипед, вписанный в шар Теорема: Сфера может быть описана около параллелепипеда тогда и только тогда, когда параллелепипед прямоугольный, так как в данном случае он является прямым и около его основания - параллелограмма может быть описана окружность (т. к. основание - прямоугольник).

Конус и цилиндр, вписанные в шар Теорема: Около всякого конуса можно описать сферу. Теорема: Около любого цилиндра можно описать сферу.

Задача 1 Найти радиус шара, описанного правильного тетраэдра с ребром а. около Решение: Предварительно построим на изображении правильного тетраэдра SABC изображение центра описанного шара. Проведем апофемы SD и AD (SD = AD). В равнобедренном треугольнике ASD каждая точка медианы DN равноудалена от концов отрезка AS. Поэтому точка O 1 есть пересечение высоты SO и отрезка DN. Используя формулу из R 1 = b 2/(2 h), получим: SO 1 = SA 2/(2 SO); SO = SO 1 = a 2/(2 a =a =)=a /4. Ответ: SO 1 = a /4.

Задача 2 В правильной четырехугольной пирамиде сторона основания равна а, а плоский угол при вершине равен α. Найти радиус описанного шара. Решение: По формуле R 1=b 2/(2 h) для нахождения радиуса описанного шара найдем SC и SO. SC = a/(2 sin(α/2)); SO 2). (a/(2 sin(α/2))2 – (a /2)2 = =). = a 2/(4 sin 2(α/2)) – 2 a 2/4 = = a 2/(4 sin 2(α/2)) · (1 – 2 sin 2(α/2)) = = a 2/(4 sin 2(α/2)) · cosα R 1 = a 2/(4 sin 2(α/2)) · 1/(2 a Ответ: R 1 = a/(4 sin(α/2) · /(2 sin(α/2))) = a/(4 sin(α/2) ·

Многогранники, описанные около шара Выпуклый многогранник называется описанным, если все его грани касаются некоторой сферы. Эта сфера называется вписанной для данного многогранника. Центром вписанной сферы является точка, равноудаленная от всех граней многогранника.

Положение центра вписанной сферы Понятие биссекторной плоскости двугранного угла. Биссекторной называется плоскость, делящая двугранный угол на два равных двугранных угла. Каждая точка этой плоскости равноудалена от граней двугранного угла. В общем случае центр вписанной в многогранник сферы является точкой пересечения биссекторных плоскостей всех двугранных углов многогранника. Он всегда лежит внутри многогранника.

Пирамида, описанная около шара Шар, называется вписанным в (произвольную) пирамиду, если он касается всех граней пирамиды (как боковых, так и основания). Теорема: Если боковые грани одинаково наклонены к основанию, то в такую пирамиду можно вписать шар. Так как двугранные углы при основании равны, то их половинки тоже равны биссектрисы пересекаются в одной точке на высоте пирамиды. Эта точка принадлежит всем биссекторным плоскостям при основании пирамиды и равноудалена от всех граней пирамиды – центр вписанного шара.

Формула для нахождения радиуса вписанной сферы Пусть SABC - пирамида с равными боковыми ребрами, h - ее высота, r радиус вписанной окружности. Найдем радиус описанной сферы. Пусть SO = h, OH = r, O 1 O = r 1. Тогда по свойству биссектрисы внутреннего угла треугольника O 1 O/OH = O 1 S/SH; r 1/r = (h – r 1)/ ; r 1 · = rh – rr 1; r 1 · (+ r) = rh; r 1 = rh/(+ r). Ответ: r 1 = rh/(+ r).

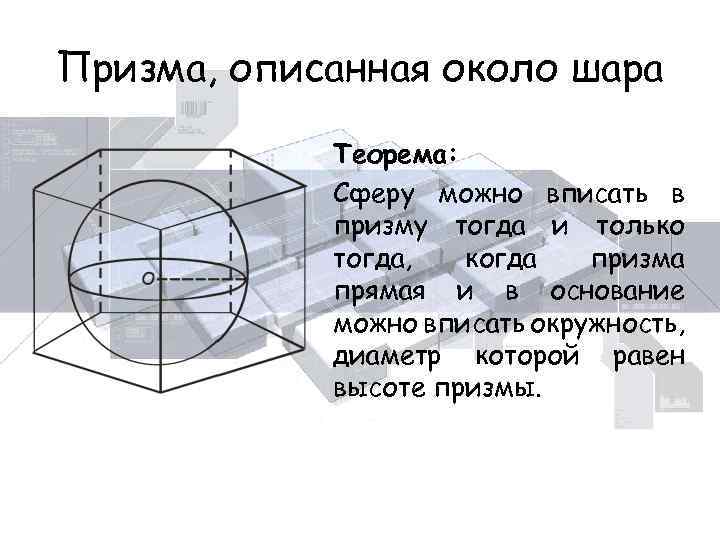Призма, описанная около шара Теорема: Сферу можно вписать в призму тогда и только тогда, когда призма прямая и в основание можно вписать окружность, диаметр которой равен высоте призмы.

Параллелепипед и куб, описанные около шара Теорема: В параллелепипед можно вписать сферу тогда и только тогда, когда параллелепипед прямой и его основание ромб, причем высота этого ромба есть диаметр вписанной сферы, который, в свою очередь, равен высоте параллелепипеда. (Из всех параллелограммов только в ромб можно вписать окружность) Теорема: В куб всегда можно вписать сферу. Центр этой сферы точка пересечения диагоналей куба, а радиус равен половине длины ребра куба.

Цилиндр и конус, описанные около шара Теорема: Сферу можно вписать лишь в такой цилиндр, высота которого равна диаметру основания. Теорема: Во всякий конус можно вписать сферу.

Комбинации фигур Вписанная и описанная призмы Призма, вписанная в цилиндр – призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковыми ребрами – образующие цилиндра. Касательная плоскость к цилиндру – плоскость, проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую. Призма, описанная около цилиндра – призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковые грани касаются цилиндра.

Вписанная и описанная пирамиды Пирамида, вписанная в конус – пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершиной является вершина конуса. Боковые ребра пирамиды, вписанной в конус – образующие конуса. Касательная плоскость к конусу – плоскость, проходящая через образующую и перпендикулярная плоскости осевого сечения, содержащей эту образующую. Пирамида, описанная около конуса – пирамида, у которой основанием служит многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса. Плоскости боковых граней описанной пирамиды – касательные плоскости конуса.

Другие виды конфигураций Цилиндр вписан в пирамиду, если окружность одного его основания касается всех боковых граней пирамиды, а другое его основание лежит на основании пирамиды. Конус вписан в призму, если его вершина лежит на верхнем основании призмы, а его основание – круг, вписанный в многоугольник – нижнее основание призмы. Призма вписана в конус, если все вершины верхнего основания призмы лежат на боковой поверхности конуса, а нижнее основание призмы лежит на основании конуса.

Задача 1 В правильной четырехугольной пирамиде сторона основания равна а, а плоский угол при вершине равен α. Найдите радиус вписанного в пирамиду шара. Решение: Выразим стороны ∆SOK через а и α. OK = a/2. SK = KC · ctg(α/2); SK = (a · ctg(α/2))/2. SO = = (a/2) Использую формулу r 1 = rh/(+ r), найдем радиус вписанного шара: r 1 = OK · SO/(SK + OK); r 1 = (a/2) · (a/2) /((a/2) · ctg(α/2) + (a/2)) = = (a/2) /(ctg(α/2) + 1) = (a/2) Ответ: r 1 = (a/2) =

Вывод Тема «Многогранники» изучается учениками в 10 и 11 классах, но в учебной программе очень мало материала на тему «Вписанные и описанные многогранники» , хотя она вызывает очень большой интерес у учащихся, так как изучение свойств многогранников способствует развитию абстрактного и логического мышления, что впоследствии пригодится нам в учебе, работе, жизни. Работая над данным рефератом, мы изучили весь теоретический материал на тему «Вписанные и описанные многогранники» , рассмотрели возможные комбинации фигур и научились применять весь изученный материал на практике. Задачи на комбинацию тел – наиболее трудный вопрос курса стереометрии 11 класса. Но теперь мы с уверенностью можем сказать, что у нас не возникнет проблем при решении подобных задач, так как в ходе нашей исследовательской работы мы установили и доказали свойства вписанных и описанных многогранников. Очень часто у учащихся возникают трудности при построении чертежа к задаче на данную тему. Но, узнав, что для решения задач на комбинацию шара с многогранником изображение шара бывает излишним и достаточно указать его центр и радиус, мы можем быть уверены, что данных трудностей у нас не возникнет. Благодаря данному реферату мы смогли разобраться в этой трудной, но очень увлекательной теме. Мы надеемся, что теперь у нас не возникнет трудностей применении изученного материала на практике.

Тип урока: Урок ознакомления с новым материалом.

Цели урока:

Ввести понятие сферы, вписанной в многогранник; сферы, описанной около многогранника.

Сравнить описанную окружность и описанную сферу, вписанную окружность и вписанную сферу.

Проанализировать условия существования вписанной сферы и описанной сферы.

Сформировать навыки решения задач по теме.

Развитие у учащихся навыков самостоятельной работы.

Развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности.

Скачать:

Предварительный просмотр:

Описанная окружность.

Определение: Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника , а многоугольник – вписанным в окружность.

Теорема. Около любого треугольника можно описать окружность и притом только одну.

В отличие от треугольника около четырехугольника не всегда можно описать окружность. Например: ромб.

Теорема. В любом вписанном четырехугольнике сумма противоположных углов равна 180 0 .

Если сумма противоположных углов четырехугольника равна 180 0 , то около него можно описать окружность.

Для того чтобы четырехугольник АВСD был вписанным, необходимо и достаточно, выполнения любого из следующих условий:

• ABCD выпуклый четырехугольник и ∟ABD=∟ACD;
• Сумма двух противоположных углов четырехугольника равна 180 0 .

Центр окружности равноудален от каждой из его вершин и поэтому совпадает с точкой пересечения серединных перпендикуляров к сторонам многоугольника, а радиус равен расстоянию от центра до вершин.

Для треугольника: Для правильного многоугольника:

Вписанная окружность.

Определение: Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

Теорема. В любой треугольник можно вписать окружность и притом только одну.

Не во всякий четырехугольник можно вписать окружность. Например: прямоугольник, не являющийся квадратом.

Теорема. В любом описанном четырехугольнике суммы длин противоположных сторон равны.

Если суммы длин противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Для того чтобы выпуклый четырехугольник ABCD являлся описанным, необходимо и достаточно, чтобы выполнялось условие AB+DC=BC+AD (суммы длин противоположных сторон равны).

Центр окружности равноудален от сторон многоугольника, значит, совпадает с точкой пересечения биссектрис углов многоугольника (свойство биссектрисы угла). Радиус равен расстоянию от центра окружности до сторон многоугольника.

Для треугольника: Для правильного

Многоугольника:

Предварительный просмотр:

Вписанная сфера.

Определение: Сфера называется вписанной в многогранник, если она касается всех граней многогранника. Многогранник в таком случае называется описанным около сферы.

Центр вписанной сферы – точка пересечения биссекторных плоскостей всех двугранных углов.

Сфера называется вписанной в двугранный угол, если она касается его граней. Центр вписанной в двугранный угол сферы лежит на биссекторной плоскости этого двугранного угла. Сфера называется вписанной в многогранный угол, если она касается всех граней многогранного угла.

Не во всякий многогранник можно вписать сферу. Например: в прямоугольный параллелепипед, не являющийся кубом, сферу вписать нельзя.

Теорема . В любую треугольную пирамиду можно вписать сферу и притом только одну.

Доказательство. Рассмотрим треугольную пирамиду CABD. Проведем биссекторные плоскости ее двугранных углов с ребрами AС и BC. Они пересекаются по прямой, которая пересечет биссекторную плоскость двугранного угла с ребром АВ. Таким образом, биссекторные плоскости двугранных углав с ребрами АВ,АС и ВС имеют единственную общую точку. Обозначим ее Q. Точка Q равноудалена от всех граней пирамиды. Следовательно, сфера соответствующего радиуса с центром в точке Q является вписанной в пирамиду САBD.

Докажем ее единственность. Центр любой сферы вписанной в пирамиду CABD равноудален от ее граней, значит, он принадлежит биссекторным плоскостям двугранных углов. Следовательно, центр сферы совпадает с точкой Q. Что требовалось доказать.

Теорема. В пирамиду, у которой в основание можно вписать окружность, центр которой служит основанием высоты пирамиды, можно вписать сферу.

Следствие. В любую правильную пирамиду можно вписать сферу.

Докажите, что центр сферы вписанной в правильную пирамиду, лежит на высоте этой пирамиды (докажите самостоятельно).

Центр сферы, вписанной в правильную пирамиду, есть точка пересечения высоты пирамиды с биссектрисой угла, образованного апофемой и ее проекцией на основание.

Задача. а , высота равна h.

Решите задачу.

Задача. 0

Предварительный просмотр:

Описанная сфера.

Определение. Сфера называется описанной около многогранника, если________________________________________ ___________________________________________________________________________________________________________. Многогранник при этом называется _______________________________________.

Каким свойством обладает центр описанной сферы?

Определение. Геометрическим местом точек пространства, равноудаленных от концов некоторого отрезка, является ___________________________________________________________________________________________________________ ___________________________________________________________________________________________________________.

Приведите пример многогранника, около которого нельзя описать сферу: ________________________ __________________________________________________________________________________________________________ .

Около какой пирамиды можно описать сферу?

Теорема. ____________________________________________________________________________________________ ____________________________________________________________________________________________________ .

Доказательство. Рассмотрим треугольную пирамиду ABCD. Построим плоскости, перпендикулярные соответственно ребрам АВ, АС и AD и проходящие через их середины. Обозначим через О точку пересечения этих плоскостей. Такая точка существует, и она единственна. Докажем это. Возьмем первые две плоскости. Они пересекаются, поскольку перпендикулярны непараллельным прямым. Обозначим прямую, по которой пересекаются первые две плоскости, через l . Эта прямая l перпендикулярна плоскости АВС. Плоскость, перпендикулярная AD, не параллельна l и не содержит ее, поскольку в противном случае прямая AD перпендикулярна l , т.е. лежит в плоскости АВС. Точка О равноудалена от точек А и В, А и С, А и D, значит, она равноудалена ото всех вершин пирамиды ABCD, т. е. сфера с центром в О соответствующего радиуса является описанной сферой для пирамиды.

Докажем ее единственность. Центр любой сферы, проходящей через вершины пирамиды, равноудален от этих вершин, значит, он принадлежит плоскостям, которые перпендикулярны ребрам пирамиды и проходят через середины этих ребер. Следовательно, центр такой сферы совпадает с точкой О. Теорема доказана.

Около какой еще пирамиды можно описать сферу?

Теорема. _____________________________________________________________________________________________ ___________________________________________________________________________________________________________ ___________________________________________________________________________________________________________ ___________________________________________________________________________________________________________.

Центр сферы, описанной около пирамиды, совпадает с точкой пересечения прямой, перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности и плоскости, перпендикулярной любому боковому ребру, проведенной через середину этого ребра.

Для того чтобы около многогранника можно было описать сферу необходимо, __________________________________ ___________________________________________________________________________________________________________.

При этом центр описанной сферы может лежать ___________________________________________________________ ___________________________________________________________________________________________________________ и проектируется в центр описанной около любой грани окружности; перпендикуляр, опущенный из центра описанной около многогранника сферы на ребро многогранника, делит это ребро пополам.

Следствие. ___________________________________________________________________________________________ ___________________________________________________________________________________________________________ .

Центр сферы, описанной около правильной пирамиды, лежит ________________________________________________ ___________________________________________________________________________________________________________.

Проанализируйте решение задачи.

Задача. В правильной четырехугольной пирамиде сторона основания равна а , высота равна h. Найдите радиус сферы, описанной около пирамиды.

Решите задачу.

Задача. 0

Предварительный просмотр:

Открытый урок по теме «Вписанные и описанные многогранники»

Тема урока: Сфера, вписанная в пирамиду. Сфера, описанная около пирамиды.

Тип урока: Урок ознакомления с новым материалом.

Цели урока:

• Развитие у учащихся навыков самостоятельной работы.
• Развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;

Оборудование:

• Интерактивная доска
• Презентация «Вписанная и описанная сфера»
• Условия задач в рисунках на доске.
• Раздаточный материал (опорные конспекты).

1. Планиметрия. Вписанная и описанная окружность.
2. Стереометрия. Вписанная сфера
3. Стереометрия. Описанная сфера

Структура урока:

• Постановка целей урока (2 минуты).
• Подготовка к изучению нового материала повторением (фронтальный опрос) (6 минут).
• Объяснение нового материала (15 минут)
• Осмысление темы при самостоятельном составлении конспекта по теме «Стереометрия. Описанная сфера» и применение темы при решении задач (15 минут).
• Подведение итогов урока проверкой знания и понимания изученной темы (фронтальный опрос). Оценка ответов учащихся (5 минут).
• Постановка домашнего задания (2 минуты).
• Резервные задания.

Ход урока

1. Постановка целей урока.

• Ввести понятие сферы, вписанной в многогранник; сферы, описанной около многогранника.
• Сравнить описанную окружность и описанную сферу, вписанную окружность и вписанную сферу.
• Проанализировать условия существования вписанной сферы и описанной сферы.
• Сформировать навыки решения задач по теме.

2. Подготовка к изучению нового материала повторением (фронтальный опрос).

Окружность, вписанная в многоугольник.

• Какая окружность называется вписанной в многоугольник?
• Как называется многоугольник, в который вписана окружность?
• Какая точка является центром окружности, вписанной в многоугольник?
• Каким свойством обладает центр окружности, вписанной в многоугольник?
• Где располагается центр окружности, вписанной в многоугольник?
• Какой многоугольник можно описать около окружности, при каких условиях?

Окружность, описанная около многоугольника.

• Какая окружность называется описанной около многоугольника?
• Как называется многоугольник, около которого описана окружность?
• Какая точка является центром окружности, описанной около многоугольника?
• Каким свойством обладает центр окружности, описанной около многоугольника?
• Где может располагаться центр окружности, описанной около многоугольника?
• Какой многоугольник можно вписать в окружность и при каких условиях?

3. Объяснение нового материала.

А . По аналогии учащиеся формулируют новые определения и отвечают на поставленные вопросы.

Сфера, вписанная в многогранник.

• Сформулируйте определение сферы, вписанной в многогранник.
• Как называется многогранник, в который можно вписать сферу?
• Каким свойством обладает центр вписанной в многогранник сферы?
• Что представляет множество точек пространства, равноудаленных от граней двугранного угла? (трехгранного угла?)
• Какая точка является центром сферы, вписанной в многогранник?
• В какой многогранник можно вписать сферу, при каких условиях?

В . Учащиеся доказывают теорему.

В любую треугольную пирамиду можно вписать сферу.

В процессе работы на уроке учащиеся пользуются опорными конспектами.

С. Учащиеся анализируют решение задачи.

В правильной четырехугольной пирамиде сторона основания равна а , высота равна h. Найдите радиус сферы, вписанной в пирамиду.

D. Учащиеся решают задачу.

Задача. В правильной треугольной пирамиде сторона основания равна 4, боковые грани наклонены к основанию под углом 60 0 . Найдите радиус, вписанной в эту пирамиду сферы.

4. Осмысление темы при самостоятельном составлении конспекта по « Сфера, описанная около многогранника » и применение при решении задач.

А. У чащиеся самостоятельно заполняют конспект по теме «Сфера, описанная около многогранника». Отвечают на следующие вопросы:

• Сформулируйте определение сферы, описанной около многогранника.
• Как называется многогранник, около которого можно описать сферу?
• Каким свойством обладает центр описанной около многогранника сферы?
• Что представляет собой множество точек пространства, равноудаленных от двух точек?
• Какая точка является центром сферы, описанной около многогранника?
• Где может быть расположен центр сферы, описанной около пирамиды? (многогранника?)
• Около какого многогранника можно описать сферу?

В. Учащиеся самостоятельно решают задачу.

Задача. В правильной треугольной пирамиде сторона основания равна 3, а боковые ребра наклонены к основанию под углом 60 0 . Найдите радиус описанной около пирамиды сферы.

С. Проверка составленного конспекта и анализ решения задачи.

5. Подведение итогов урока проверкой знания и понимания изученной темы (фронтальный опрос). Оценка ответов учащихся.

А. Учащиеся самостоятельно подводят итоги урока.

В. Отвечают на дополнительные вопросы.

• Можно ли описать сферу около четырехугольной пирамиды, в основании которой лежит ромб, не являющийся квадратом?
• Можно ли описать сферу около прямоугольного параллелепипеда? Если да, то где находится его центр?
• Где в жизни применяется изученная на уроке теория (архитектура, сотовая телефонная связь, геостационарные спутники, система обнаружения GPS).

6. Постановка домашнего задания.

А. Составить конспект по теме «Сфера, описанная около призмы. Сфера, вписанная в призму». (Рассмотреть по учебнику задачи: №632,637,638)

В. Решить из учебника задачу № 640.

С. Из методички Б.Г. Зив «Дидактические материалы по геометрии 10 класс» решить задачи: Вариант №3 С12(1), Вариант №4 С12(1).

D. Дополнительное задание: Вариант №5 С12 (1).

7. Резервные задания.

Из методички Б.Г. Зив «Дидактические материалы по геометрии 10 класс»решить задачи: Вариант №3 С12(1), Вариант №4 С12(1).

Учебно – методический комплект

1. Геометрия, 10-11: Учебник для общеобразовательных учреждений. Базовый и профильный уровни/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др., М.: Просвещение, 2010г.
2. Б.Г. Зив «Дидактические материалы по геометрии 10 класс», М.: Просвещение.

   Повторение Окружность, описанная около многоугольника Какая окружность называется описанной около многоугольника? Что является центром окружности, описанной около многоугольника? Каким свойством обладает центр окружности, описанной около многоугольника? Где располагается центр окружности, описанной около многоугольника? Какой многоугольник можно вписать в окружность и при каких условиях?

   Повторение Окружность, вписанная в многоугольник Какая окружность называется вписанной в многоугольник? Что является центром окружности, вписанной в многоугольник? Каким свойством обладает центр окружности, вписанной в многоугольник? Где располагается центр окружности, вписанной в многоугольник? Какой многоугольник можно описать около окружности, при каких условиях?

   Сфера, вписанная в многогранник Сформулируйте определение сферы, вписанной в многогранник. Как называется многогранник? Каким свойством обладает центр вписанной сферы? Где расположено множество точек пространства, равноудаленных от граней двугранного угла? (трехгранного угла)? В какой многогранник можно вписать сферу?

   Сфера, вписанная в пирамиду

   Сфера, описанная около многогранника Сформулируйте определение сферы, описанной около многогранника. Как называется многогранник? Каким свойством обладает центр описанной сферы? Где расположено множество точек пространства, равноудаленных от двух точек? Где расположен центр сферы, описанной около пирамиды? (многогранника?) Около какого многогранника можно описать сферу?

   Сфера, описанная около пирамиды

   Подведение итогов урока. Можно ли описать сферу около четырехугольной пирамиды, в основании которой лежит ромб, не являющийся квадратом? Можно ли описать сферу около прямоугольного параллелепипеда? Если да, то где находится его центр?

   Домашнее задание. Составить конспект по теме «Сфера, описанная около призмы. Сфера, вписанная в призму». (Рассмотреть по учебнику задачи: №632,637,638) Решить из учебника задачу № 640. Из методички решить задачи: Вариант №3 С12(1), Вариант №4 С12(1).

   
   

   Определение. Сфера называется вписанной в многогранник , если плоскости всех граней многогранника касаются сферы в тачках, расположенных внутри этих граней. При этом многогранник называется описанным около сферы.

   Теорема 1. В произвольный тетраэдр можно вписать сферу (шар).

   Множество точек, равноудаленных от боковых граней тетраэдра есть прямая пересечения двух биссекторных плоскостей двугранных углов при двух боковых ребрах. Эту прямую пересечет биссекторная плоскость двугранного угла при основании. Полученная точка равноудалена от всех граней тетраэдра.

   В тетраэдре ABCD плоскости CDN и ADM являются биссекторными плоскостями двугранных углов при боковых ребрах CD и AD. Они пересекаются по прямой OD. Плоскость AKC является бисссекторной плоскостью двугранного угла при основании (ребро AC). Эта плоскость пересечет прямую OD в точке S (P – точка пересечения прямых DM и KC, принадлежащая плоскостям AKC и ADM одновременно, следовательно точка S – точка пересечения AP и OD), которая будет являться точкой, равноудаленной от всех граней тетраэдра и, следовательно, будет являться центром сферы, вписанной в тетраэдр ABCD.

   Пример 1 . Найти радиус сферы, вписанной в правильный тетраэдр.

   Рассмотрим подобные треугольники DPS и DOK (по двум углам: угол D – общий, углы DPS и DOK – прямые).

   Тогда PS:KO=DS:DK,

   если учесть, что PS=r=SO и DS=DO-SO=DO-r,

   

   , , то .

   Ответ: радиус сферы, вписанной в правильный тетраэдр равен

   Теорема 2. В правильную пирамиду можно вписать сферу.

   Теорема 3. В правильную усеченную пирамиду можно вписать сферу тогда и только тогда, когда ее апофема равна сумме радиусов окружностей, вписанных в ее основания.

   Теорема 4. В любую призму можно вписать сферу, если в ее перпендикулярное сечение можно вписать окружность, радиус которой равен половине высоты призмы.

   Теорема 5. В правильную призму можно вписать сферу тогда и только тогда, когда высота призмы равна диаметру окружности, вписанной в ее основание.

   Сферы, описанные около цилиндра, конуса и

   
   
   

   Усеченного конуса.

   Определение. Сфера называется описанной около цилиндра или усеченного конуса , если все точки окружностей оснований принадлежат сфере; Сфера называется описанной около конуса , если все точки окружности основания, а также вершина конуса принадлежат сфере.

   В этих случаях говорят, что цилиндр, усеченный конус или конус вписан в сферу.

   Теорема 1. Около произвольного цилиндра можно описать сферу.

   

   О 1 и О 2 – центры нижнего и верхнего основания соответственно. Прямая О 1 О 2 перпендикулярна плоскостям основания. Проведем плоскость, проходящую через середину образующей цилиндра, перпендикулярно этой образующей. Эта плоскость будет параллельна плоскостям основания и пересекать прямую О 1 О 2 в точке О, которая и будет являться центром сферы, описанной около цилиндра. Расстояние от точки О до всех точек основания будет равным, так как О 1 О 2 является ГМТ, равноудаленных от окружности (прямая, проходящая через центр окружности и перпендикулярна плоскости окружности). Значит точка О является центром сферы с радиусом ОА, описанной около цилиндра.

   Теорема 2. Около усеченного конуса можно описать сферу.

   

   О 1 и О 2 – центры нижнего и верхнего основания соответственно. Прямая О 1 О 2 перпендикулярна плоскостям основания. Рассмотрим образующую усеченного конуса АВ. Найдем ГМТ, равноудаленных от тачек А и В. Им будет являть плоскость, проходящая через точку Р – середину АВ и перпендикулярная этой прямой. Эта плоскость пересечет О 1 О 2 в точке О, которая будет равноудалена от точек А и В. Также очевидно, что точка О будет равноудалена от все точек оснований усеченного конуса. Следовательно эта точка О будет являться центром сферы с радиусом ОА, описанной около усеченного конуса.

   Теорема 3. Около конуса можно описать сферу.

   

   Аналогично прошлой теореме ОА – высота конуса, которая является ГМТ, равноудаленных от окружности. Рассмотрим образующую АВ и найдем ГМТ, равноудаленных от А и В. Полученная плоскость (по предыдущей задаче) пересечет ОА в точке О 1 , которая будет равноудалена от точек А и В, как и от любых точек основания конуса. Таким образом мы получили, что точка О 1 является центром сферы с радиусом О 1 А, описанной около конуса.

   
   

   
   

   
   

   Многогранники, вписанные в шар Выпуклый многогранник называется вписанным, если все его вершины лежат на некоторой сфере. Эта сфера называется описанной для данного многогранника. Центр этой сферы является точкой, равноудаленной от вершин многогранника. Она является точкой пересечения плоскостей, каждая из которых проходит через середину ребра многогранника перпендикулярно ему.
   

   
   

   
   

   
   

   Формула для нахождения радиуса описанной сферы Пусть SABC - пирамида с равными боковыми ребрами, h - ее высота, R - радиус окружности, описанной около основания. Найдем радиус описанной сферы. Заметим подобие прямоугольных треугольников SKO1 и SAO. Тогда SO 1 /SA = KS/SO; R 1 = KS · SA/SO Но KS = SA/2. Тогда R 1 = SA 2 /(2SO); R 1 = (h 2 +R 2)/(2h); R 1 = b 2 /(2h), где b - боковое ребро.
   

   
   

   
   

   
   

   Параллелепипед, вписанный в шар Теорема: Сфера может быть описана около параллелепипеда тогда и только тогда, когда параллелепипед прямоугольный, так как в данном случае он является прямым и около его основания - параллелограмма - может быть описана окружность (т. к. основание - прямоугольник).
   

   
   

   
   

   
   

   Задача 1 Найти радиус шара, описанного около правильного тетраэдра с ребром а. Решение: SO 1 = SA 2 /(2SO); SO = = = a SO 1 = a 2 /(2 a) = a /4. Ответ:SO 1 = a /4. Предварительно построим на изображении правильного тетраэдра SABC изображение центра описанного шара. Проведем апофемы SD и AD (SD = AD). В равнобедренном треугольнике ASD каждая точка медианы DN равноудалена от концов отрезка AS. Поэтому точка O 1 есть пересечение высоты SO и отрезка DN. Используя формулу из R 1 = b 2 /(2h), получим:
   

   
   

   Задача 2 Решение: По формуле R 1 =b 2 /(2h) для нахождения радиуса описанного шара найдем SC и SO. SC = a/(2sin(α /2)); SO 2 = (a/(2sin(α /2)) 2 – (a /2)2 = = a 2 /(4sin 2 (α /2)) – 2a 2 /4 = = a 2 /(4sin 2 (α /2)) · (1 – 2sin 2 (α /2)) = = a 2 /(4sin 2 (α /2)) · cos α В правильной четырехугольной пирамиде сторона основания равна а, а плоский угол при вершине равен α. Найти радиус описанного шара. R 1 = a 2 /(4sin 2 (α /2)) · 1/(2a/(2sin(α /2))) =a/(4sin(α /2) ·). Ответ: R 1 = a/(4sin(α /2) ·).
   

   
   

   Многогранники, описанные около шара Выпуклый многогранник называется описанным, если все его грани касаются некоторой сферы. Эта сфера называется вписанной для данного многогранника. Центром вписанной сферы является точка, равноудаленная от всех граней многогранника.
   

   
   

   Положение центра вписанной сферы Понятие биссекторной плоскости двугранного угла. Биссекторной называется плоскость, делящая двугранный угол на два равных двугранных угла. Каждая точка этой плоскости равноудалена от граней двугранного угла. В общем случае центр вписанной в многогранник сферы является точкой пересечения биссекторных плоскостей всех двугранных углов многогранника. Он всегда лежит внутри многогранника.
   

   
   

   Пирамида, описанная около шара Шар, называется вписанным в (произвольную) пирамиду, если он касается всех граней пирамиды (как боковых, так и основания). Теорема: Если боковые грани одинаково наклонены к основанию, то в такую пирамиду можно вписать шар. Так как двугранные углы при основании равны, то их половинки тоже равны биссектрисы пересекаются в одной точке на высоте пирамиды. Эта точка принадлежит всем биссекторным плоскостям при основании пирамиды и равноудалена от всех граней пирамиды – центр вписанного шара.
   

   
   

   Формула для нахождения радиуса вписанной сферы Пусть SABC - пирамида с равными боковыми ребрами, h - ее высота, r - радиус вписанной окружности. Найдем радиус описанной сферы. Пусть SO = h, OH = r, O 1 O = r 1. Тогда по свойству биссектрисы внутреннего угла треугольника O 1 O/OH = O 1 S/SH; r 1 /r = (h – r 1)/ ; r 1 · = rh – rr 1 ; r 1 · (+ r) = rh; r 1 = rh/(+ r). Ответ: r 1 = rh/(+ r).
   

   
   

   
   

   
   

   Параллелепипед и куб, описанные около шара Теорема: В параллелепипед можно вписать сферу тогда и только тогда, когда параллелепипед прямой и его основание - ромб, причем высота этого ромба есть диаметр вписанной сферы, который, в свою очередь, равен высоте параллелепипеда. (Из всех параллелограммов только в ромб можно вписать окружность) Теорема: В куб всегда можно вписать сферу. Центр этой сферы - точка пересечения диагоналей куба, а радиус равен половине длины ребра куба.
   

   
   

   
   

   
   

   Комбинации фигур Вписанная и описанная призмы Призма, описанная около цилиндра – призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковые грани касаются цилиндра. Призма, вписанная в цилиндр – призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковыми ребрами – образующие цилиндра. Касательная плоскость к цилиндру – плоскость, проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
   

   
   

   Вписанная и описанная пирамиды Пирамида, вписанная в конус – пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершиной является вершина конуса. Боковые ребра пирамиды, вписанной в конус – образующие конуса. Пирамида, описанная около конуса – пирамида, у которой основанием служит многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса. Плоскости боковых граней описанной пирамиды – касательные плоскости конуса. Касательная плоскость к конусу – плоскость, проходящая через образующую и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
   

   
   

   Другие виды конфигураций Цилиндр вписан в пирамиду, если окружность одного его основания касается всех боковых граней пирамиды, а другое его основание лежит на основании пирамиды. Конус вписан в призму, если его вершина лежит на верхнем основании призмы, а его основание – круг, вписанный в многоугольник – нижнее основание призмы. Призма вписана в конус, если все вершины верхнего основания призмы лежат на боковой поверхности конуса, а нижнее основание призмы лежит на основании конуса.
   

   
   

   Задача 1 В правильной четырехугольной пирамиде сторона основания равна а, а плоский угол при вершине равен α. Найдите радиус вписанного в пирамиду шара. Решение: Выразим стороны SOK через а и α. OK = a/2. SK = KC · ctg(α /2); SK = (a · ctg(α /2))/2. SO = = (a/2) Использую формулу r 1 = rh/(+ r), найдем радиус вписанного шара: r 1 = OK · SO/(SK + OK); r 1 = (a/2) · (a/2) /((a/2) · ctg(α /2) + (a/2)) = = (a/2) /(ctg(α /2) + 1) = (a/2)= = (a/2) Ответ: r 1 = (a/2)
   

   
   

   Вывод Тема «Многогранники» изучается учениками в 10 и 11 классах, но в учебной программе очень мало материала на тему «Вписанные и описанные многогранники», хотя она вызывает очень большой интерес у учащихся, так как изучение свойств многогранников способствует развитию абстрактного и логического мышления, что впоследствии пригодится нам в учебе, работе, жизни. Работая над данным рефератом, мы изучили весь теоретический материал на тему «Вписанные и описанные многогранники», рассмотрели возможные комбинации фигур и научились применять весь изученный материал на практике. Задачи на комбинацию тел – наиболее трудный вопрос курса стереометрии 11 класса. Но теперь мы с уверенностью можем сказать, что у нас не возникнет проблем при решении подобных задач, так как в ходе нашей исследовательской работы мы установили и доказали свойства вписанных и описанных многогранников. Очень часто у учащихся возникают трудности при построении чертежа к задаче на данную тему. Но, узнав, что для решения задач на комбинацию шара с многогранником изображение шара бывает излишним и достаточно указать его центр и радиус, мы можем быть уверены, что данных трудностей у нас не возникнет. Благодаря данному реферату мы смогли разобраться в этой трудной, но очень увлекательной теме. Мы надеемся, что теперь у нас не возникнет трудностей при применении изученного материала на практике.
   

   Многогранники, вписанные в сферу Многогранник называется вписанным в сферу, если все его вершины принадлежат этой сфере. Сама сфера при этом называется описанной около многогранника. Теорема. Около пирамиды можно описать сферу тогда и только тогда, когда около основания этой пирамиды можно описать окружность.

   
   

   Многогранники, вписанные в сферу Теорема. Около прямой призмы можно описать сферу тогда и только тогда, когда около основания этой призмы можно описать окружность. Ее центром будет точка O, являющаяся серединой отрезка, соединяющего центры окружностей, описанных около оснований призмы. Радиус сферы R вычисляется по формуле где h – высота призмы, r – радиус окружности, описанной около основания призмы.
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   Упражнение 3 Основанием пирамиды служит правильный треугольник, сторона которого равна 3. Одно из боковых ребер равно 2 и перпендикулярно плоскости основания. Найдите радиус описанной сферы. Решение. Пусть O – центр описанной сферы, Q – центр окружности, описанной около основания, E – середина SC. Четырехугольник CEOQ – прямоугольник, в котором CE = 1, CQ = Следовательно, R=OC=2. Ответ: R = 2.
   

   
   

   Упражнение 4 На рисунке изображена пирамида SABC, для которой ребро SC равно 2 и перпендикулярно плоскости основания ABC, угол ACB равен 90 о, AC = BC = 1. Постройте центр сферы, описанной около этой пирамиды и найдите ее радиус. Решение. Через середину D ребра AB проведем прямую, параллельную SC. Через середину E ребра SC проведем прямую параллельную CD. Их точка пересечения O будет искомым центром описанной сферы. В прямоугольном треугольнике OCD имеем: OD = CD = По теореме Пифагора, находим
   

   
   

   Упражнение 5 Найдите радиус сферы, описанной около правильной треугольной пирамиды, боковые ребра которой равны 1, и плоские углы при вершине равны 90 о. Решение. В тетраэдре SABC имеем: AB = AE = SE = В прямоугольном треугольнике OAE имеем: Решая это уравнение относительно R, находим
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   Упражнение 4 Найдите радиус сферы, описанной около прямой треугольной призмы, в основании которой прямоугольный треугольник с катетами, равными 1, и высота призмы равна 2. Ответ: Решение. Радиус сферы равен половине диагонали A 1 C прямоугольника ACC 1 A 1. Имеем: AA 1 = 2, AC = Следовательно, R =
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   Упражнение Найдите радиус сферы, описанной около правильной 6-угольной пирамиды, ребра основания которой равны 1, а боковые ребра - 2. Решение. Треугольник SAD – равносторонний со стороной 2. Радиус R описанной сферы равен радиусу окружности, описанной около треугольника SAD. Следовательно,
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   Упражнение Найдите радиус сферы, описанной около единичного икосаэдра. Решение. В прямоугольнике ABCD AB = CD = 1, BC и AD – диагонали правильных пятиугольников со сторонами 1. Следовательно, BC = AD = По теореме Пифагора AC = Искомый радиус равен половине этой диагонали, т.е.
   

   
   

   
   

   
   

   Упражнение Найдите радиус сферы, описанной около единичного додекаэдра. Решение. ABCDE – правильный пятиугольник со стороной В прямоугольнике ACGF AF = CG = 1, AC и FG – диагонали пятиугольника ABCDE и, следовательно, AC = FG = По теореме Пифагора FC = Искомый радиус равен половине этой диагонали, т.е.
   

   
   

   
   

   
   

   Упражнение На рисунке изображен усеченный тетраэдр, получаемый отсечением от углов правильного тетраэдра треугольных пирамид, гранями которого являются правильные шестиугольники и треугольники. Найдите радиус сферы, описанной около усеченного тетраэдра, ребра которого равны 1.
   

   
   

   
   

   
   

   
   

   
   

   
   

   
   

   Упражнение На рисунке изображен усеченный октаэдр, получаемый отсечением от углов октаэдра треугольных пирамид, гранями которого являются правильные шестиугольники и треугольники. Найдите радиус сферы, описанной около усеченного октаэдра, ребра которого равны 1. Упражнение На рисунке изображен усеченный икосаэдр, получаемый отсечением от углов икосаэдра пятиугольных пирамид, гранями которого являются правильные шестиугольники и пятиугольники. Найдите радиус сферы, описанной около усеченного икосаэдра, ребра которого равны 1.
   Упражнение На рисунке изображен усеченный додекаэдр, получаемый отсечением от углов додекаэдра треугольных пирамид, гранями которого являются правильные десятиугольники и треугольники. Найдите радиус сферы, описанной около усеченного додекаэдра, ребра которого равны 1.
   Упражнение Найдите радиус сферы, описанной около единичного кубооктаэдра. Решение. Напомним, что кубооктаэдр получается из куба отсечением правильных треугольных пирамид с вершинами в вершинах куба и боковыми ребрами, равными половине ребра куба. Если ребро октаэдра равно 1, то ребро соответствующего куба равно Радиус описанной сферы равен расстоянию от центра куба до середины его ребра, т.е. равен 1. Ответ: R = 1.